h32j00

이번 글에서는 블록 암호에 이어서 스트림 암호를 공부해보도록 하겠습니다!!

​

스트림 암호는 블록 암호보다 취약하고 더 자주 깨졌다는 이유로 꺼리는 사람들이 있었는데요 지금은 다행히 안전한 스트림 암호를 설계하는 방법이 알려져 있고, 블루투스 연결, 이동전화의 4G 통신, TLS 연결 등이 스트림 암호 덕분에 안전하게 보호된다고 합니다!

​

5.1 스트림 암호의 작동 방식

스트림 암호는 DRBG( 결정론적 난수 비트 발생기 )처럼 결정론적이다. 스트림 암호와 DRBG의 차이는 DRBG는 하나의 값을 입력받지만 스트림 암호는 두 개의 값( 키, 논스(nonce) )을 입력받는다.

키는 반드시 비밀, 논스는 비밀일 필요는 없다.

스트림 암호의 암호화 방식

암호화 방식을 살펴 보면, 키와 논스를 입력 받아 스트림 암호 알고리즘을 통해 키스트림(KS)을 생성한다. 키스트림과 평문 P를 XOR 하면 암호문이 나오고, 그 암호문을 다시 키스트림과 XOR 하면 평문이 나온다.

스트림 암호에서 키와 논스는 각각 재사용이 가능하지만 같이 재사용을 하면 이전과 동일한 KS가 생성되므로 동시에 재사용은 하면 안된다.

​

5.1.1 상태 있는 스트림 암호와 카운터 기반 스트림 암호

크게 봤을 때, 스트림 암호는 상태 있는 스트림 암호(stateful stream cipher)와 카운터 기반 스트림 암호(counter-based stream cipher)로 나뉜다.

i ) 상태 있는 스트림 암호 ex) RC4

주어진 키와 논스로 상태를 초기화(init) 한 후 갱신 함수(update)를 통해서 상태값을 갱신하고, 상태로 부터 하나 이상의 키 스트림 비트들을 생성하고 평문과 XOR 해서 암호문을 얻는다.

​

ii ) 카운터 기반 스트림 암호

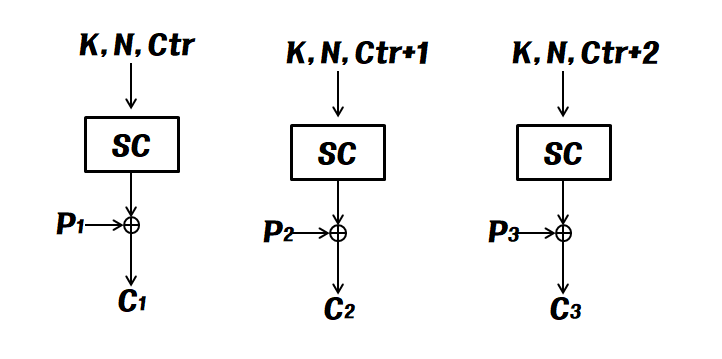
키와 논스, 카운터 값을 이용해서 키스트림 조각들을 생성한다.

​

스트림 암호의 내부는 대상 플랫폼에 따라 크게 두 범주로 나뉜다. 하나는 하드웨어 지향적 스트림 암호, 다른 하나는 소프트웨어 지향적 스트림 암호이다.

​

5.2 하드웨어 지향적 스트림 암호

암호의 하드웨어 구현은 암복호화 이외의 용도로는 쓰이지 않는다.

초창기 스트림 암호들은 복잡한 워드 단위 연산을 피하기 위해 비트들을 다루었기 때문에 하드웨어에서 더 효율적이었다. 또한 블록 암호보다 구현 비용이 낮아서 잘 쓰였었는 데 현재는 블록 암호가 스트림 암호보다 비싸지 않다. 그렇긴 하지만, 예전에 하드웨어에 대해 최고의 선택이었다는 이유로 지금도 스트림 암호를 하드웨어와 연관 시키는 경우가 많다.

​

5.2.1 FSR(되먹임 자리이동 레지스터)

되먹임 함수를 f 라고 하고 FSR의 각 갱신 연산에서는 그 상태의 값을 변경하고 하나의 출력 비트를 산출한다.

식으로 나타내보자면

Rt+1 = (Rt << 1) | f(Rt)

여기서 | 는 OR 이고 << 는 왼쪽으로 shift 이다.

ex) 되먹임 함수 f는 주어진 네 비트를 XOR로 결합하는 함수, 초기 상태 : 1 1 0 0

f(1100) = 1 xor 1 xor 0 xor 0 = 0

새로운 상태 : (1100<<1) | 0 = 1000

이런 식으로 계속해나가면

1100 -> 1000 -> 0001 -> 0011-> 0110 -> 1100 이렇게 되어서 주기(period)가 5가 된다.

보안을 위해서는 이러한 반복 패턴을 피해야 하며 주기가 길어야 한다.

​

i ) LFSR(선형 되먹임 자리이동 레지스터)

되먹임 함수가 선형 함수인 FSR이다.

암호학에서 선형성은 예측가능성과 같은 말이다. 바탕에 깔린 수학 구조가 단순함.

LFSR의 주기는 되먹임 함수가 레지스터의 어떤 비트들을 XOR하느냐에 크게 의존. -> 최대 주기인 2^n-1이 나오도록 비트들을 선택하는 방법이 알려져 있음.

만약 1번째, 3번째, 4번째 비트들을 xor 한다고 하면 다항식을 1+X^1+X^3+X^4 로 만들 수 있고 이렇게 만든 다항식이 원시다항식(기약다항식, 즉 더 이상 인수분해할 수 없는 다항식)이면 FSR의 주기가 최대가 된다.

1+X^1+X^3+X^4 = (1+X)(1+X^3) 이므로 원시다항식이 아님.

벌러캠프-매시 알고리즘(Berlekamp-Massey algorithm) 이용해서 LFSR의 수학 구조로 정의된 방정식들을 풀 수 있어서 LFSR은 안전하지 않다.

​

ii ) 필터링된 LFSR

LFSR이 출력한 비트들을 비선형함수로 변환한다면 LFSR의 선형성을 숨길 수 있고, 비보안성을 완화시킬 수 있을 것이다. 이러한 LFSR을 필터링된 LFSR이라고 부른다.

그림에서 g 함수는 반드시 비선형 함수여야 한다. -> XOR 뿐만 아니라 AND, OR 연산으로도 결합

하지만 아래의 공격을 이용하면 이 암호체계를 깰 수 있다.

1) 대수적 공격(algebraic attack) : 출력 비트들로부터 비선형 방정식들을 연역해서 푼다.

2) 큐브 공격(cube attack)​ : 비선형 방정식들의 도함수를 계산해서 방정식들의 차수를 1까지 끌어내린다.

3) 고속 상관 공격(fast correlation attack) : 비선형성을 가지고 있긴 하지만 선형함수처럼 행동하는 경향이 있는 필터링 함수들을 활용한다.

​

iii ) NFSR(비선형 FSR)

LFSR과 비슷하지만 되먹임 함수가 비선형이다.

장점 : 암호학적으로 강해진다

단점 : NFSR의 주기를 효율적으로 알아내는 것이 불가능하다.

주기가 짧으면 LFSR과 NFSR을 결합해서 최대 주기를 보장하고 암호학적 강도도 보장해서 사용 -> Grain-128a

​

5.2.2 Grain-128a

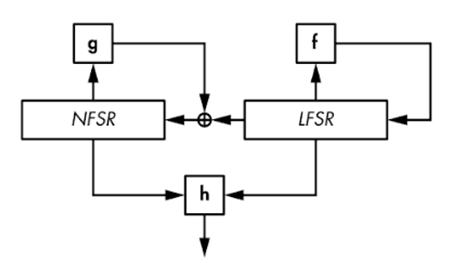
Grain-128a는 128비트 키와 96비트 논스를 사용한다.

128비트 키는 NFSR의 128비트 레지스터에 복사, 96비트 논스의 비트들은 LFSR 레지스터의 앞부분 96비트에 복사하고 나머지 32 비트 중 31개의 비트에는 1로 마지막 비트는 0으로 설정한다. 초기화 단계에서는 시스템 전체를 256번 갱신하고 그 다음에야 첫 번째 키스트림 비트를 출력한다.

<LFSR의 되먹임 함수>

f(L) = L32 + L47 + L58 + L90 + L121 + L128

<NFSR의 되먹임 함수>

g(N) = N32 + N37 + N72 + N102 + N128 + N44N60 + N61N125 + N63N67 + N69N101 + N80N88 + N110N111 + N115N117 + N46N50N58 + N103N104N106 + N33N35N36N40

필터 함수 h 역시 비선형함수이다. 이 함수는 NFSR에서 비트 9개, LFSR에서 비트 7개를 받아서 적절히 결합한다.

h(x) = bi+12 Si+8 + Si+13Si+20 + bi+95Si+42 + Si+60Si+79 + bi+12bi+95Si+94

​

5.2.3 A5/1

A5/1은 2G 이동통신 표준에서 음성 통신을 암호화하는 데 쓰였던 스트림 암호이다.

​

- A5/1의 작동 방식

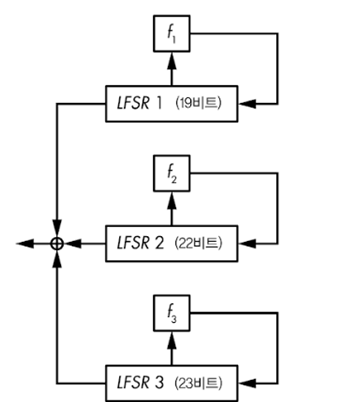
그림에서 보듯이 A5/1은 비트 수가 각각 19, 22, 23인 LFSR들을 사용한다.

< 되먹임 다항식 >

LFSR 1 = 1 + X^14 + X^17 + X^18 + X^19

LFSR 2 = 1 + X^21 + X^22

LFSR 3 = 1 + X^8 + X^21 + X^22 + X^23

< 갱신 매커니즘 >

1. LFSR 1의 비트 9의 값, LFSR 2의 비트 11의 값, LFSR 3의 비트 11의 값이 모두 같거나 한 비트만 다르다. 이 비트들을 클로킹 비트 ( clocking bit ) 라고 한다.

2. 만약 클로킹 비트가 1 1 1 이면 1의 클로킹 비트를 가지고 있는 레지스터끼리 xor을 하고 1 0 0 이면 0이 더 많으니까 0의 클로킹 비트를 가지고 있는 레지스터끼리 xor을 한다.

​

- A5/1에 대한 공격 기법

1. 정교한 공격 ( subtle attack ) : 내부 선형성, 단순한 불규칙 클로킹 체계를 활용

- 추측 후 판정 ( guess-and-determine )이라고 부르는 한 정교한 공격 기법에서 공격자는 상태의 특정 비밀 값들을 추측해서 다른 비밀 값들을 알아낸다.

↓ 이러한 공격을 나타낸 의사코드다.

LFSR 1의 초기 상태의 모든 가능한 2^19가지 값에 대해: LFSR 2의 초기 상태의 모든 가능한 2^22가지 값에 대해: 처음 11 클록 동안 LFSR 3의 클로킹 비트의 모든 가능한 2^11가지 값에 대해: LFSR 3의 초기 상태를 재구축한다. 추측이 맞는지 점검한다. 맞으면 반환하고 아니면 반복한다.

LFSR 1의 초기 상태의 모든 가능한 2^19가지 값에 대해: 
	LFSR 2의 초기 상태의 모든 가능한 2^22가지 값에 대해: 
    		처음 11 클록 동안 LFSR 3의 클로킹 비트의 모든 가능한 2^11가지 값에 대해: 
        		LFSR 3의 초기 상태를 재구축한다. 
            		추측이 맞는지 점검한다. 맞으면 반환하고 아니면 반복한다.

2. 무차별 공격 ( brutal attack ) : 짧은 키와 프레임 번호 주입의 가역성 활용

- 코드북 공격을 함. -> 실제로 2G 이동통신의 암호문을 코드북 공격을 이용해서 거의 실시간으로 복호화할 수 있었다.

​

5.3 소프트웨어 지향적 스트림 암호

현대적인 CPU는 비트에 대한 연산에 걸리는 시간과 워드에 대한 연산에 걸리는 시간이 다를 바가 없기 때문에 바이트나 워드를 다루는 것이 더 효율적이다. 그래서 소프트웨어 스트림 암호가 하드웨어 암호보다 더 낫다. 현재 암호학자들이 가장 주목하는 설계 두 가지는 RC4와 Salsa20이다.

​

5.3.1 RC4

오랫동안 가장 널리 쓰인 스트림 암호인 RC4는 역공학을 통해 취약점이 노출되었다.

최초의 Wi-Fi 암호화 표준인 WEP ( Wired Equivalent Privacy; 유선 동등 프라이버시 ) 와 HTTPS 연결에 쓰이는 TLS ( Transport Layer Security; 전송 계층 보안 ) 프로토콜에 사용됐다.

​

- RC4의 작동 방식

RC4의 내부 상태인 256개의 바이트로 이루어진 배열 S를 키 K를 이용해서 초기화한다. -> 키 스케줄링 알고리즘

S의 두 인덱스를 선택해서 swap 하고 두 특정 바이트를 통해 키스트림을 생성한다. 여기서 얻은 키스트림을 평문 P와 XOR 하여 암호문을 얻는다.

j=0 
S = range(256) 
for i in range(256): 
	j = (j + S[i] + K[i%n]) % 256 
   	S[i], S[j] = S[j], S[i]

i = 0
j = 0 
for b in range(m):
	i = (i + 1) % 256
   	j = (j + S[i]) % 256
   	S[i], S[j] = S[j], S[i]
   	KS[b] = S[(S[i] + S[j]) % 256]

위의 코드에서 m은 평문의 길이이고 그 길이 만큼 swap을 진행한다. 이 방식을 테이블 셔플링(shuffling) 방식이라고 한다.

​

- WEP의 RC4

: 무선망으로 자료를 전송하는 데이터그램인 802.11 프레임 안에 있는 페이로드 자료를 암호화한다. 한 세션에서 전송되는 모든 페이로드 자료는 40, 104 비트 길이의 동일한 비밀 키 사용. 각 페이로드 헤더에는 3 바이트 논스 값이 부호화되어있다.

여기서 문제!! RC4는 논스를 지원하지 않는다. -> WEP 설계자들은 무선 프레임 헤더에 24비트 논스를 포함하고 그것을 RC4의 비밀 키로 쓰이는 WEP 키의 앞에 붙였다.

* WEP의 논스 편법의 진정한 문제점

1. 논스가 너무 작다.

2. 논스와 키를 연결하는 방식 때문에 키를 복원하기 쉽다.

​

- TLS의 RC4

: TLS는 인터넷에서 쓰이는 가장 중요한 보안 프로토콜이다. HTTPS 연결의 용도로 널리 알려져 있지만 그 뿐아니라 VPN이나 이메일 서버, 이동통신 응용 프로그램 등의 여러 응용을 보호하는 데에도 쓰인다.

TLS의 약점은 전적으로 RC4 때문이다. -> 통계적 편향, 비무작위성

​

5.3.2 Salsa20

Salsa20은 현대적인 CPU에 최적화된 간단한 소프트웨어 지향적 스트림 암호이다.

Salsa20은 하나의 키 K와 하나의 논스 N, 카운터 값 Ctr로 이루어진 512 비트 블록을 핵심(core) 알고리즘을 이용해서 변환하고 그 결과를 원래 512비트 블록과 더해서 하나의 키스트림 블록을 산출한다.

​

- 쿼터 라운드 함수

이 함수는 네 개의 32비트 워드(a,b,c,d)를 다음과 같이 변환

b = b xor [(a + d) <<< 7]

c = c xor [(b + a) <<< 9]

d = d xor [(c + b) <<< 13]

a = a xor [(d + c) <<< 18]

​

- Salsa20의 512비트 상태의 변환

Salsa20 초기 상태

C0~C3 : 상수

K0~K7 : 키

V0, V1 : 논스

T0, T1 : 카운터

​

<변환 과정>

1. 열 라운드(column-round) - 홀수번째 라운드

2. 행 라운드(row-round) - 짝수번째 라운드

열 라운드와 행 라운드의 조합을 이중 라운드(double-round) -> salsa20은 이중 라운드를 10번 반복(2x10 = 20)

​

- Salsa20의 평가 : 10라운드 반복 후 무작위해 보이지만 그 자체가 보안성을 보장하지는 않는다.

하지만 RC4보다는 훨씬 안전하며, 통계적 편향이 없다.

​

- 차분 암호해독 : 상태들의 실제 값 자체가 아니라 상태들의 차이를 연구하는 차분 암호해독(differential cryptanalysis)

차분 암호해독으로 살펴본 결과 비트 하나 차이가 512 비트 상태의 거의 모든 비트로 전파되는 걸 확인할 수 있는 데 이 성질을 전확산(full diffusion)이라고 부른다.

상태의 진화가 XOR와 덧셈, 순환 자리 이동의 조합으로 이루어진 고도로 비선형적인 관계식이면 공격자가 미래의 상태 차이를 예측하기 어려워진다.

​

- Salsa20/8에 대한 공격

Salsa20/8은 라운드를 8회만 수행하는 버전으로 2^256회 미만의 연산으로 키를 복원하는 공격 기법이다.

통계적 편향을 활용하며 논스 N, 카운터 Ctr, 키 K를 알면 키스트림 계산을 거꾸로 수행해서 초기 상태를 복원할 수 있다.

키의 일부를 제대로 추측 -> 편향된 비트가 나타남 ( 편향된 비트가 나타났다? 추측한 키가 맞다 )

실제 공격시, 추측이 옳은지 판정하려면 키의 비트 220개가 필요하며 키스트림 블록들의 쌍 2^31개가 필요.

정확한 비트 220개를 알아낸 후에 나머지 비트 36 개는 무차별 대입 공격으로 알아내면 된다.

5.4 문제 발생 요인들

​

5.4.1 논스 재사용

: 같은 키에 대해 하나의 논스를 두 번 이상 재사용하는 바보!!

* SIV 모드 : 같은 논스를 두 번 사용해도 안전

​

5.4.2 잘못된 RC4 구현

: RC4의 알고리즘에는 swap이 사용된다. 그 때의 코드는

buf = S[i]
S[i] = S[j] 
S[j] = buf

이 때 buf라는 새로운 변수를 사용해야하는데 프로그래머들이 이를 피하기 위해 xor-swap 을 이용하여 코드를 짠다. 아래의 코드는 오류가 있는 코드의 일부이다.

#define SWAP(x,y) do {x^=y; y^=x; x^=y;} while(0)
... 
SWAP(S[i], S[j]);

이렇게 되어 있는 데 i=j 일때 문제가 생긴다.

xor swap에서 i=j이면 s[i]에 0이 배정된다. ( i와 j가 같아서 S[i]와 S[j]도 같음) -> 결국 모든 바이트가 0,,,,

​

이로써 스트림 암호도 알아봐버렸다!! 너무 어렵디만 하다보면 익숙해지겠지,, *^^*

더 열심히 해보자!! 바-위~

부스트코스에서 진행하는 "파이토치로 시작하는 딥러닝 기초"를 듣고있다.

Part 2를 끝내고 지금까지 배운 것을 가지고 패션 분류기를 만들었다.

코드를 바탕으로 정리하는 것을 목표로 글을 쓰도록 하겠다. 하지만 모든 코드는 공유할 수 없으니 기억해둘 것만,,

패션 분류기에 사용할 데이터 셋은 Fashion-Mnist이다.

Mnist와 같이 784차원의 입력과 10차원의 출력이 있다.

1. 코드 초반에는 모듈과 라이브러리들을 import 해준다.

2. batchsize, epochs, learning rate를 정해준다.

이 값들은 초기에 세팅해주는 값들인데 딥러닝을 많이 하다보면 잘 정할 수 있다고 강의에서 말씀해주셨다.

3. dataset과 dataloader를 설정해준다

데이터는 training set과 test set를 구분해서 학습, 검증해야 정확한 accuracy가 나온다.

FashionMNIST 데이터셋을 불러오기 위해 torchvision.datasets을 import 하였다.

import torchvision.datasets as datasets

train = datasets.FashionMNIST(root, train=True, transform, download)
test = datasets.FashionMNIST(root, train=False, transform, download)

train_loader = DataLoader(data, batchsize, shuffle)

이와 같이 train 의 bool 값을 기준으로 나눌 수 있다.

또한 DataLoader(데이터, batchsize, shuffle)를 이용하여 train_dataloader와 test_dataloader를 설정해준다.

4. 네트워크 및 모델 설계

이번 실습에서 사용할 네트워크는 MLP(Multi Layer Perceptron)이다.

하나의 퍼셉트론이 아닌 hidden layer를 포함한 신경망이라고 생각하면 되겠다.

이때 activation function은 ReLU를 사용한다.

다른 activation function으로는 Sigmoid가 있지만 이 함수는 미분을 계속하게되면 0으로 수렴하는 값을 내기 때문에

gradient vanishing 문제가 발생할 수 있다. 그래서 좀 덜한 ReLU를 사용한다.

각 layer 마다 입력, 출력, batch nomalization, activation function을 지정해줄 수 있다.

입력, 출력에는 특징의 갯수, 즉 차원을 써주면 되고

activation function은 사용할 활성화 함수를 써주면 된다.

batch nomalization은 뭘까?

각 layer를 지날때마다 입력된 분포와 출력된 분포가 달라지고 이에 따라 발생하는 문제를 줄이기 위해 각 mini batch마다 nomalization을 해주는 방법이다. 이 batchnorm은 activation function을 사용하기 전에 사용하는 것이 일반적이라고 한다.

모델을 설계할때는

import torch.nn as nn

model = nn.Sequential(layer, batch_norm, activation_func)

이런 형식으로 설계할 수 있고

model = model.to(device)

이런 형식으로 생성할 수 있다.

device는 gpu 또는 cpu로 설정할 수 있다.

마지막 layer의 activation function은 softmax 함수이다. (현재상황에서는)

하지만 activation_func 자리에 nn.softmax 이런식으로 쓰지않는다.

이유는 6번에서 알려주도록 하겠다.

5. weight initialization

weight initialization은 weight를 0으로 초기화하지 않고 적절한 초기화방법을 이용하여 학습의 성능을 높여줄 수 있다.

방법에는 "Restricted Boltzmann Machine", "Xavier", "He" 초기화 방법이 있는데 RBM은 복잡해서 잘 안쓰이고

간단한 Xavier, He를 쓴다. He는 Xavier의 변형된 방법이다.

import torch.nn as nn

#Xavier를 이용한 초기화
nn.init.xavier_uniform_(layer.weight) #이거 혹은
nn.init.xavier_normal_(layer.weight) #이거

6. loss function, optimizer 

딥러닝의 궁극적인 목표는 loss 값을 최소로 하는 모델을 만드는 것이다.

loss function에는 cross entropy loss, binary cross entropy 등등이 있지만 여기서의 출력값이 두가지가 아니기 때문에

cross entropy loss function을 쓰도록 했다.

import torch.nn as nn

criterion = nn.CrossEntropyLoss().to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)

이렇게 쓸 수 있다.

아까 출력 층의 activation function을 써주지 않는 이유를 말하자면

cross entropy loss function이 softmax 기능도 해주기 때문이다!!

optimizer는 gradient를 최적화 해주는 친구이다.

optimizer의 종류에는 Adam, SGD(Stochastic Gradient Descent) 등이 있는데 SGD는 Adam에 비해 느리다고 배웠다..

그래서 Adam을 사용했다. optimizer에게는 모델의 변수들과 학습률을 알려줘야한다. lr는 이미 정해둔 값이다.

7. train

training 시키는 단계이다.

epoch만큼 돌면서 batch size만큼 가져와서 학습을 시킨다. 

학습을 시키는 단계는 다음과 같다.

output = model(X) # 예측값 구하기
cost = criterion(output, Y)  # loss 값 구하기

optimizer.zero_grad() # 이전 계산된 gradient 초기화
cost.backward() # gradient 계산
optimizer.step() # 모델의 parameter들 학습

8. test

model.eval() # test 하겠다
with torch.no_grad():
	블라블라~~

이런식으로 진행한다.

torch.no_grad()는 진행하면서 gradient 학습을 하지 않겠다는 말이다.

당연한 얘기겠지??

이런 단계를 가지고 코드를 짰고

결과는

높은 accuracy를 가지고 잘 진행되었다.

내가 위에 적은 코드는 정말 최소~로 필요한 코드기 때문에 기본기만 훑었다고 생각하면 될 듯 하다.

인공지능에 대해 아무것도 몰랐지만 그래도 부스트코스덕분에 100중에 0.5는 안 것 같다. 설명 진짜 잘하신다!

땡큐 부스트코스~!~!

오늘은 블록암호에 대해 알아보자.

미국 정부에서 만든 DES(Data encryption Standard; 자료 암호화 표준), 벨기에에서 개발된 DES의 후계자 AES(Advanced Encryption Standard), KGB가 개발한 GOST 28147-89 의 공통점은 무엇일까?

바로 블록 암호(block cipher)라는 것이다.

4.1 블록 암호란 무엇인가?

하나의 블록 암호는 암호화 알고리즘 하나 + 복호화 알고리즘 하나로 구성

​

4.1.1 보안 목표

블록 암호에서의 보안성?? "얼마나 무작위하게 보이는가" --> 반드시 의사무작위 치환(pseudorandom permutation, PRP) = 키를 알지 못하는 한 공격자는 임의의 입력으로부터 블록 암호의 출력을 계산할 수 없어야 한다.

4.1.2 블록 크기

블록 암호의 보안성은 (a) 블록의 크기 , (b) 키의 크기 에 의존한다.

DES - 64(2^6)비트 블록

AES - 128(2^7)비트 블록

*현대적인 CPU들이 64비트보다 128비트를 더 효율적으로 처리하며 128비트 블록이 더 안전

* 암호문의 길이나 메모리 사용량을 최대한 아껴야 하는 상황에서는 64비트 블록을 사용할 수 있다.

4.1.3 코드북 공격

메모리를 아낀다고 블록을 너무 작게 사용한다면? 코드북 공격(codebook attack)에 당할 수 있다.

코드북 공격은 블록이 작을 때만 효율적으로 작용하는 불록 암호 공격 기법이다. -> 32비트 블록까지는 감당할 수 있지만 블록이 그것보다 더 커지면 현실적으로 불가능!

​

4.2 블록 암호 구성

블록 암호를 구성하는 데 쓰이는 기법의 수는 그리 많지 않다.

1. 실제 쓰이는 블록 암호는 하나의 거대한 알고리즘이 아닌 짧은 라운드들을 반복하는 형태의 알고리즘이다.

2. 라운드를 구축하는 기법은 크게 두가지이다. ( 대입-치환 네트워크, 파이스텔 방안 )

​

4.2.1 블록 암호의 라운드

블록 암호의 알고리즘은 명세와 구현이 쉬운 기본적인 형태의 라운드를 여러 번 반복하는 것으로 구성된다.

ex) 평문을 세 개의 라운드로 암호화하는 블록 암호를 C = R3(R2(R1(P)))로 표현

- 각 라운드마다 서로 다른 라운드 키 존재.

- 각 라운드는 동일한 알고리즘을 사용하되 라운드 키로 매개변수 되서 다른 라운드 키를 가지면 다른 동작을 하게 된다.

- 각 라운드 키는 주 키 K 로부터 생성 ( 키 스케줄 알고리즘 사용 ), 주 키 K와는 다른 값.

4.2.2 슬라이드 공격과 라운드 키

모든 라운드가 같아버리면 어떤 일이 일어날까? 슬라이드 공격(slide attack)에 당하게 된다..

위 사진에서는 라운드가 세개라 C2=R(C1) 만 알수 있지만 라운드 수가 늘어나도 항상 성립한다.

공격자가 한 라운드의 입력과 출력을 알아내서 키 복원에 활용할 수 있다.

따라서 라운드 마다 다른 라운드 키를 사용해야 이런 슬라이드 공격을 좌절시킬 수 있다.

4.2.3 대입-치환 네트워크 ( substitution-permutation network, SPN )

- 혼돈(confusion) : 입력(평문과 암호화 키)이 복잡한 변환들을 거친다, 깊이에 관한 것

- 확산(diffusion) : 그러한 변환들이 모든 비트에 동일하게 의존한다, 너비에 관한 것

- 대입 연산은 대입 상자(substitution box; S-상자)로 구현된다.

* 대입 상자 : 4비트 또는 8비트의 자료 조각을 변환하는 작은 참조표

- 치환은 그냥 비트들의 순서를 바꾸는 정도로 간단한 치환일 수도 있지만 비트들을 많이 뒤섞진 못한다. 대신 어떤 암호들은 기본적인 선형대수와 행렬 곱셈을 이용해서 비트들을 섞는다.

* 대입-치환 네트워크 알고리즘을 사용하는 대표적인 암호는 AES이다. 뒤에서 자세히 알아보도록 하자.

​

4.3.4 파이스텔 방안 ( Feistel scheme )

- 파이스텔 방안의 작동 과정

1. 일단 암호화하려는 정보를 절반으로 잘라서 (L, R) 을 얻는다.

2. L = L xor F(R) // F는 하나의 대입-치환 라운드

3. L과 R을 교환하여 (R,L)을 얻는다

4. 단계 2와 3을 15번 되풀이 한다.

5. L과 R을 연결해서 하나의 64비트 출력 블록을 만든다.

이런 방식으로 동작을 한다. F 함수들이 받는 Ki는 라운드 마다 다르고 48비트 라운드 키이다.

여기서 F는 의사무작위 함수(PRP)일 수도 있고, 의사난수 함수(pseudorandom function, PRF)일 수도 있다.

- PRP : 서로 다른 두 입력에 대해 각각 다른 출력을 산출

- PRF : 서로 다른 두 입력에 대해 같은 출력을 할 수도 있다. ( F가 암호학적으로 강한 함수면 이러한 차이는 무시 )

* 이론적으로 F가 왕왕 강하다면 라운드가 4개만 있어도 충분하지만 현실은 그보다 많은 수의 라운드 사용.

4.3 AES(고급 암호화 표준)

* AES는 현재 이 세상에서 가장 많이 쓰이는 암호다.

​

4.3.1 AES의 내부

- AES는 128비트 블록들을 128비트나 192, 256비트 비밀 키 하나를 이용해서 처리한다.

- 가장 널리 쓰이는 것은 128비트. ( 대부분의 응용 프로그램에서 128비트와 256비트의 보안성 차이는 무의미 )

AES는 하나의 16바이트 평문을 2차원 배열로 취급한다. 이 배열을 AES의 내부 상태 (internal "state")

AES는 같은 구조의 SPN과 다수의 라운드를 사용해서 상태를 변환

위 그림에서 보듯이, 하나의 AES 라운드는 4가지 연산으로 이루어져 있음.

1) SubBytes : 각 바이트(S0, ... , S15)를 대입 상자에 따라 다른 바이트로 대체한다.

2) ShiftRows : 0에서 3 까지의 i에 대해, i번째 행을 i자리 만큼 순환 이동.

3) MixColumns : 상태의 네 열(column)에 대해 동일한 선형변환을 적용. ( 선형변환 : 예측가능 )3

4) AddRoundKey : 라운드 키와 내부 상태의 XOR.

* KeyExpansion이 없으면? 모든 라운드 키가 같음 -> 슬라이드 공격에 취약

* AddRoundKey가 없으면? 누구나 키 없이도 임의의 암호문을 복호화

* SubBytes가 없으면? 한 열의 변화가 다른 열들에 영향을 미치지 않아서 코드북 만들어 깰 수 있음

* MixColumns가 없으면? 참조표를 이용해서 암호문을 복호화할 수 있음

** 복호화 하는 과정은 모든 연산의 역함수 이용

4.4 AES의 구현

4.4.1 테이블 기반 구현

4.4.2 전용 기계어 명령

4.4.3 AES는 안전한가?

AES는 블록 암호가 안전할 수 있을 만큼 안전하며, 절대 깨지지 않는다.

왜냐하면 모든 출력 비트가 모든 입력 비트에 어떤 복잡하고도 의사무작위한 방식으로 의존하기 때문이다.

하지만 AES가 모든 가능한 공격에 면역이라는 증명은 없다. ( 우리가 모든 가능한 공격을 모르기 때문에 )

그리고 블록 암호에 대한 가장 큰 위협은 핵심 알고리즘이 아니라 "운영 모드"들에 존재한다.

​

4.5 운영 모드

4.5.1 전자 코드북(ECB) 모드

블록 암호의 암호화에서 가장 간단한 모드!!

하지만 안전하지 않으므로 사용하면 안 된다! -> 같은 키와 같은 평문으로 암호화를 반복하면 같은 암호문이 나옴, 전체 블록 단위의 자료들만 처리할 수 있음

* ECB 암호화는 원래 이미지와 색만 다른 이미지를 산출할 뿐이다.

​

4.5.2 암호 블록 연쇄(CBC) 모드

ECB와는 달리 CBC(Cipher block chaining) 모드는 Ci = E(K,Pi xor Ci-1) 로 암호화한다.

첫 블록 P1을 암호화할 때는 이전 암호문 블록이 없으므로 무작위 초기치(initial value, IV)를 사용.

CBC 모드의 복호화는 암호화와 달리 병렬 처리가 가능하여 더 빠르다.

Pi = D(K,Ci) xor Ci-1

위의 식으로 복호화 될 때 모든 암호문을 알고 있기 때문에 병렬계산과 함께 평문을 얻어낼 수 있다.

​

4.5.3 CBC 모드에서 임의의 길이의 메시지를 암호화하는 방법

EBC 모드의 단점 중 블록 단위 제약을 극복하는 방법 ( 블록 길이의 정수배가 아닌 길이의 평문 처리 방법 )을 두 가지 기법을 통해 알아보도록 하자.

1) 메시지 채우기(padding)

- 마지막 블록이 완전히 '채워질' 때 까지 평문에 여분의 바이트들을 추가한다.

- 블록들을 채우고 15 바이트를 더 채워야 하면 그 값을 0f(십진수로 15)로 메시지 끝에 15개 추가

- 블록들을 채우고 13 바이트를 더 채워야 하면 그 값을 0d(십진수로 13)로 메세지 끝에 13개 추가

- 만약 블록 길이 16의 정수배에 해당하면 그대로 끝내는 게 아닌 10(십진수로 16)로 메세지 끝에 16개 추가

* 복호화 방법

1. 모든 블록(채우기된 상태)을 복호화한다.

2. 마지막 바이트들을 살펴본다. 01이 1개 있는지, 02가 2개 있는지 등등..

3. 혹시 그렇지 않다면 복호화 거부를 하고, 과정2를 만족한다면 채움 바이트를 제거하고 평문 바이트를 돌려준다.

2) 암호문 훔치기(ciphertext stealing)

- 채우기보다 더 복잡하고 덜 쓰이지만 3가지 장점이 있다.

1. 평문이 비트 단위의 길이라서 131비트 같은 평문을 암호화할 수 있다.

2. 암호문이 평문과 같은 길이이다.

3. 채움 오라클 공격에 취약하지 않다.

그림에서도 볼 수 있듯이 C2 = P3 xor (이전 암호문 블록의 마지막 비트들) 그 다음 암호화한 결과

C3 = 이전 암호문 블록의 처음 비트들

- 단점 : 별다른 문제점이 없지만, 별로 우아하지 않고 제대로 구현하기가 어렵다.

​

4.5.4 카운터(CTR) 모드

- 암호문 훔치기의 장점을 유지하면서 단점을 피하고 싶을 때 사용하는 모드

- 블록이라는 개념에 의존하지 않고 그냥 비트들을 받아서 비트들을 산출하는 형태의 암호로 바꾸는 역할

N(논스)은 한 번만 쓰이는 수(number used only once)인 일종의 토큰값으로 한 메시지의 모든 블럭은 같은 논스 값 사용

Ctr(카운터)은 하나의 메시지들이 같은 값을 사용할 수는 없다.

- 동작 과정 : N과 Ctr을 이어붙인 다음 암호화를 해서 나온 값과 평문을 xor 해서 암호문 블록을 만든다. ( 복호화 과정도 이와 동일하기 때문에 하나의 암호화 알고리즘을 암복호화에 사용할 수 있다. )

- 논스가 무작위일 필요가 없지만 각 암호화마다 고유(유일)해야한다.

- 장점 : 그 어떤 모드보다도 빠를 수 있다. ( 병렬화 and 평문 메시지가 주어지기 전에 암호화 시작 가능 )

​

4.6 문제 발생 요인들

블록 암호에 대한 공격 중 두 가지는 반드시 알아 두어야 한다.. 라고 써있네여..

중간값 일치 공격이랑 채움 오라클 공격인데 중간값 일치 공격이랑 중간자 공격이랑 다르대여 ㅋㅋ 같은줄알았는데.. 머-쓱

​

4.6.1 중간값 일치 공격

3DES의 보안 수준이 168비트가 아닌 112비트인 이유가 중간값 일치(meet-in-the-middle, MitM) 공격 때문이다.

4.6.2 채움 오라클 공격

문제:

OEP를 구한 후 '등록성공' 으로 가는 분기점의 OPCODE를 구하시오.
정답인증은 OEP + OPCODE
EX) 00400000EB03

immunity로 열어보니

패킹이 되어있는 것을 확인할 수 있었습니다.

패킹방식은 Aspack.. UPX 툴로는 언패킹하지 못할 것 같습니다.

대신 원리를 살펴보면 패킹을 한 바이너리는

PUSHAD -> POPAD -> OEP 이런 과정을 거쳐서 원래의 entry point로 가게됩니다.

POPAD를 찾아봅시다.

POPAD를 찾고 F8을 이용해서 456501 까지 가면 PUSH 했던 445834로 뛰는 것을 볼 수 있습니다. 이 곳이 OEP라고 할 수 있겠습니다.

445834로 가봤더니 이런식으로 되어있는데 ctrl + A 나 Analysis -> Analyse code 를 누르면 

이렇게 어셈블리어를 보실 수 있습니다.

여기서 문자열을 확인해보면

( 문자열 확인법은 ->

2020/02/23 - [Forensics/Reversing] - [CodeEngn 06] Basic RCE L06 )

뭔가 성공을 이야기하는 문자열이 보입니다. Enter나 더블클릭으로 가줍니다.

분기문의 OPCODE는 7555가 되겠네요.

그 조건을 만족 못할 시에는 '등록성공'으로 못갈 것 같습니다.

답: 004458347555

랜만에 DFC 문제를 풀어보겠습니다~

영어 잘하는 제가 한번 해석을 해보자면... 큼큼 IR ... 으흠흠..... 말웨어에 감염된 pc의 $MFT 파일을 주겠다..

공격자가 $Recycle.Bin 폴더를 가지고 공격을 진행했으니 그 부분을 보면 되겠네요.

$MFT를 winhex로 열어봤습니다.

($Recycle.Bin 검색 후 살펴 봄) MFT entry 구조에 대해서 잠시 보자면

로 되어있었습니다.

$INDEX_ROOT를 좀 더 살펴보면 현재 $Recycle.Bin 폴더에는 

가 존재합니다.

생각을 해보자면 휴지통에 파일을 임의적으로 넣으면 파일명이 그대로 살아있고 ( 7.exe 처럼 )

그게아니라 일반적인 삭제라면 일반적으로 $I, $R 이라는 파일 두개가 생성됩니다. 아무래도 휴지통에만 넣는다는 것은 일반적인 삭제기 때문에 복구를 해야하니까 그에 대한 정보를 같이 생성하는 것 같습니다. 

여기까지만 보면 7.exe가 의심이 되긴합니다. 삭제한 파일이 아니라 임의적으로 옮겨놓은 파일이기 때문에..

하지만 좀 더 살펴보면 $INDEX_ROOT 속성 밑에 엔트리 속성이 깨진 속성을 확인할 수 있었습니다. $FILE_NAME이 깨진걸로 확인됨. ( time 4개, file size 2개, file name을 알 수 있는 속성은 $FILE_NAME 이기 때문에 )

이건 제가 *테스트 해본 결과 휴지통에서도 삭제된 파일임을 알 수 있었습니다.

이로써 의심되는 이유를 나열하자면 아래와 같습니다.

1. 7.exe

   1) 휴지통에 임의로 넣은 흔적(파일 이름으로 존재)

   Name: 7.exe

   Created Time: 2019-04-27 08:24:04

   Modified Time: 2019-04-27 08:24:04

   MFT Modified Time: 2019-04-27 08:25:17

   Last Accessed Time: 2019-04-27 08:24:04

   Allocated size of file: 0x90000

   Real size of file: 0x8f800

2. x.exe

   1) 휴지통에 임의로 넣은 흔적(파일 이름으로 존재)

   2) 휴지통에서도 삭제한 흔적(깨져있음)

   Name: x.exe

   Created Time: 2019-04-27 10:40:29

   Modified Time: 2019-04-27 10:40:29

   MFT Modified Time: 2019-04-27 10:40:40

   Last Accessed Time: 2019-04-27 10:40:29

   Allocated size of file: 0xf6000

   Real size of file: 0xf5098

여기서부터는 제가 따로 테스트한 과정입니다.

안쓰는 usb를 ntfs 파일시스템으로 포맷한 후 진행하였습니다.

E 드라이브 밑에 test라는 폴더를 만들고 그 안에 

aaaaa.txt, bbbbb.txt, ccccc.txt, ddddd.txt, eeeee.txt 라는 파일 5개를 추가했습니다.

그리고나서 winhex로 본 결과

test 폴더 밑에 $INDEX_ROOT 에 aaaaa.txt ~ eeeee.txt로 아주 잘 있습니다.

여기서 제가 ccccc.txt를 삭제해보겠습니다.

ccccc.txt가 없어지고 ddddd.txt가 올라온 모습을 확인할 수 있습니다.

$INDEX_ROOT는 B tree 구조로 되어있기 때문에 삭제되면 그에 맞게 구조가 변하기 때문에 ccccc 대신 ddddd가 올라온 것입니다.

여기서 다시한번 맨 뒤에 있는 eeeee.txt를 삭제해보겠습니다. eeeee.txt 뒤에는 아무 파일도 없는 데 어떤 변화가 나타날까요?

삭제를 했지만 그대로 존재하는 것을 확인했습니다. 물론 $INDEX_ROOT header에서 속성크기가 변한 것을 확인할 수 있었습니다(처음엔 eeeee.txt 까지 포함하는 크기에서 나중에는 위의 사진의 분홍색부분까지만 포함). 또한 시간이나 파일 사이즈, 파일 이름은 안깨졌지만 그 앞의 내용은 깨진 것을 확인할 수 있습니다. 이러한 테스트 결과 x.exe도 $Recycle.Bin 폴더에 존재하다가 삭제했다는 것을 알 수 있었습니다. 

문제:

OEP를 구하시오 Ex) 00400000

ExeinfoPE로 열어보니 UPX 방식으로 패킹되어있었다.

upx로 언패킹해보았다.

immunity debugger로 다시 실행했다.

잘 나온다.

OEP는 01012475다.

답: 01012475